Monte Carlo Tree Search (MCTS)
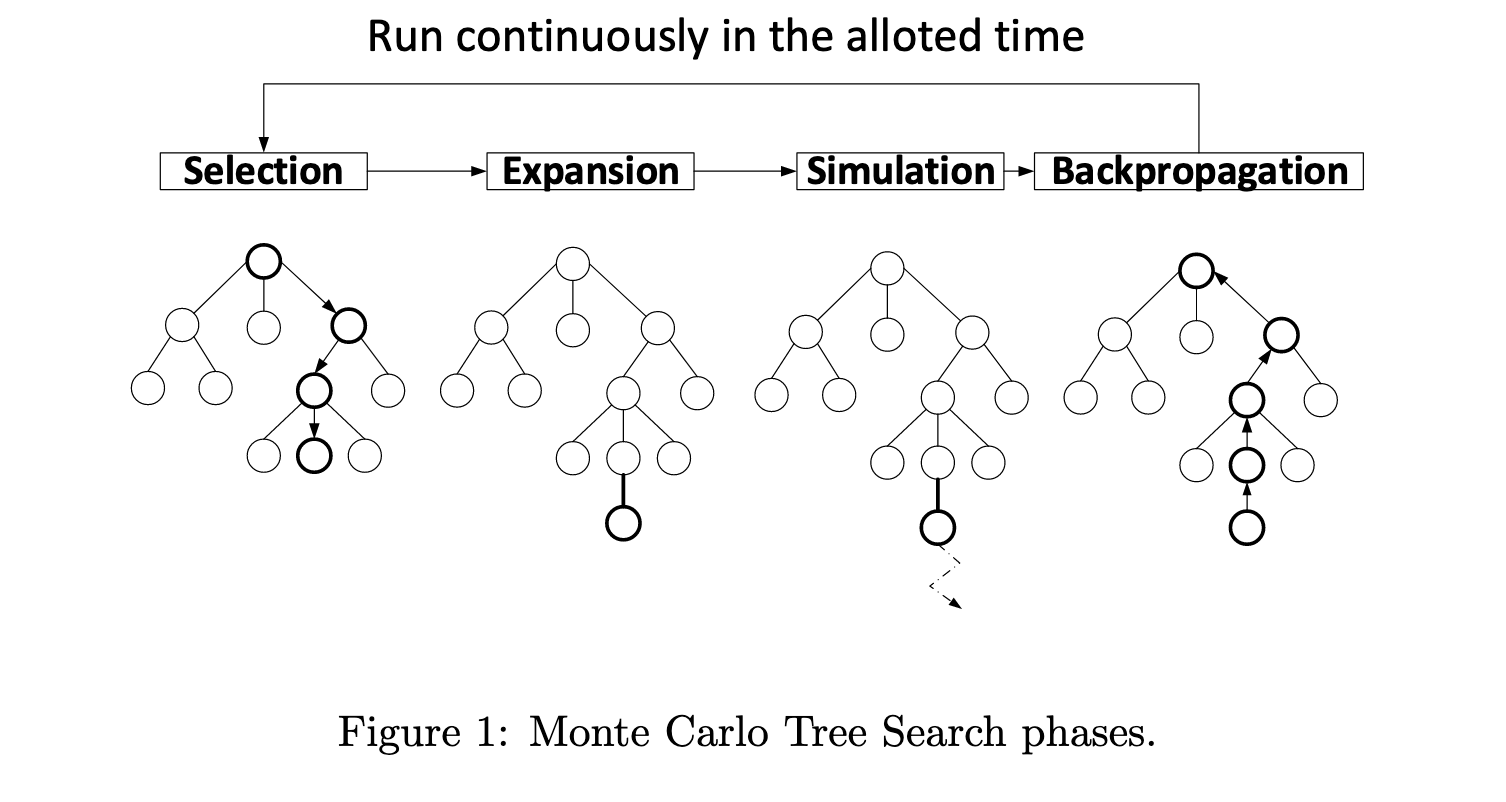
What is one iteration of MCTS?
One iteration of MCTS consists of four main steps:
- Selection: the algorithm searches the portion of the tree that has already been represented in the memory. Selection always starts from the root node and, at each level, selects the next node according to the selection policy also referred to as tree policy. This phase terminates when a leaf node is visited and the next node is either not represented in the memory yet or a terminal state of the game (problem) has been reached.
- Expansion: unless selection reached a terminal state, expansion adds at least one new child node to the tree represented in memory. The new node corresponds to a state that is reached by performing the last action in the selection phase. When expansion reaches the terminal state, which is extremely rare, then the current iteration skips directly to backpropagation.
-
Simulation (rollout/playout): performs a complete random simulation of the game/problem, i.e. reaching a terminal state and fetches the payoffs. This is the “Monte Carlo” part of the algorithm. - Backpropagation: Update the statistics in the nodes along the path from the root to the simulated terminal state based on the outcome of the simulation. This involves incrementing visit counts and updating average payoffs to reflect the results of the rollout.
What kind of problem is MCTS good at solving?
MCTS algorithm is at its core aheuristic, which means that no additional knowledge is required other than just rules of a game (or a problem, generally speaking). However, it is possible to take advantage of heuristics and include them in the MCTS approach to make it more efficient and improve its convergence. Driven by successes in games, MCTS has been increasingly often applied in domains outside the game AI such as planning, scheduling, control and combinatorial optimization.
Formally, MCTS is directly applicable to problems which can be modelled by a Markov Decision Process (MDP), which is a type of discrete-time stochastic control process. Certain modifications of MCTS make it possible to apply it to Partially Observable Markov Decision Processes (POMDP).
What is the problem formulation of MCTS?
MCTS is applicable to MDPs. MDP is a process modelled as a tuple \((S, A_S, P_a, R_a)\), where:
- \(S\) - is a set of states that are possible in an environment (state space). A specific state s0 ∈ S is distinguished as the initial state.
- \(A_s\) - denotes a set of actions available to perform in state \(s\). The subscript \(S\) can be omitted if all actions are always available in the given environment.
- \(P_a(s, s')\) - is the transition function modelled by a probability that action a performed in state s will lead to state \(s'\). In deterministic games, the probability is equal to 1 if the action in state s leads to \(s'\), whereas 0 if it does not.
- \(R_a(s)\) - is the immediate
reward (payoff)for reaching state s by action a. In Markov games, where states incorporate all the necessary information (that summarizes the history), the action component can be omitted.
What is the optimization objective of MCTS?
The optimization objective of MCTS is to find the best action to take in a given state. The best action is the one that maximizes the expected return, which is the sum of rewards that the agent can expect to accumulate over time. The expected return is calculated by averaging the rewards obtained in the simulations of the game. The best action is the one that maximizes the expected return.
\[a^* = \arg \max_{a \in A_s} Q(s, a)\]where:
- \(a^*\) - is the best action to take in state \(s\).
- \(Q(s, a)\) - is the expected return of taking action \(a\) in state \(s\).
- \(A_s\) - is a set of actions available in state \(s\).
What does memory mean in MCTS?
Memory in MCTS refers to the data structure that stores the information about the tree that represents the game states and the actions taken in the game. The memory is used to keep track of the statistics of the nodes in the tree, such as the number of visits and the average payoffs. The memory is updated during the backpropagation phase of the algorithm, where the statistics of the nodes along the path from the root to the simulated terminal state are updated based on the outcome of the simulation.
What is the tree policy/selection policy in MCTS?
The aim of the selection policy is to maintain a proper balance between the exploration (of not well-tested actions) and exploitation (of the best actions identified so far). The most common algorithm, which has become de-facto the enabler of the method is called Upper Confidence Bounds applied for Trees (UCT).
\(a^* = \arg \max_{a \in A_s} \left( Q(s, a) + c \sqrt{\frac{\log N(s)}{N(s, a)}} \right)\)
where:
- \(a^*\) - is the best action to take in state \(s\).
- \(Q(s, a)\) - is the expected return of taking action \(a\) in state \(s\).
- \(N(s)\) - is the number of times state \(s\) has been visited.
- \(N(s, a)\) - is the number of times action \(a\) has been taken in state \(s\).
- \(c\) - is a constant that controls the balance between exploration and exploitation. A common value for \(c\) is \(\sqrt{2}\).
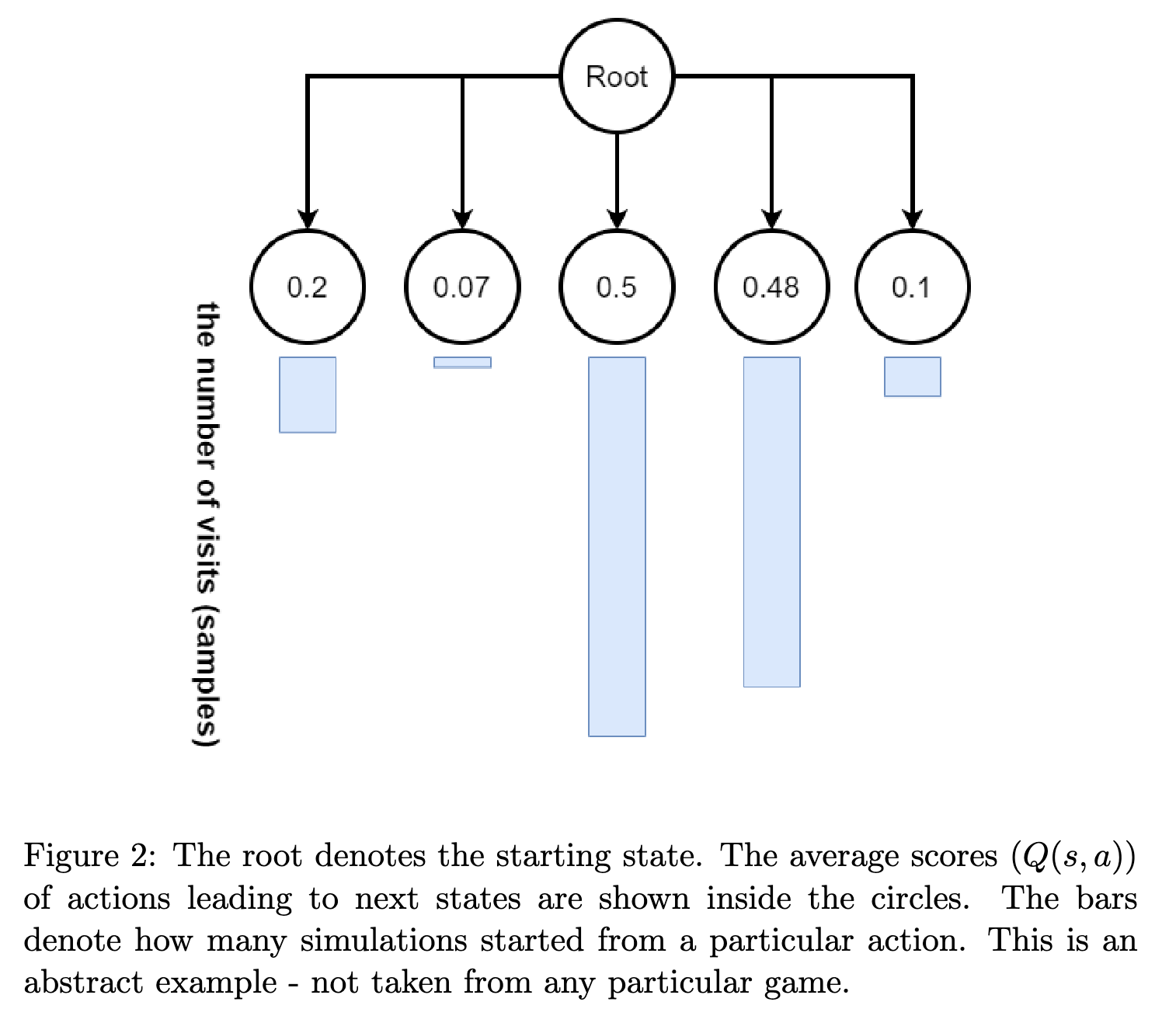
MCTS searches the game tree in an asymmetric fashion in contrast to traditional tree search methods such as minimax. The promising lines of play are searched more thoroughly.
Enjoy Reading This Article?
Here are some more articles you might like to read next: